3.2
Demand
[3.3
Price Elasticity]
[3.4 Supply]
[3.5 Production]
[3.6 Costs]
How
can you increase the demand for your company's product? How will your
competitor's production and pricing decisions affect the demand for your
product? How will raising the price of your product by $20 affect your sales?
What determines the prices of the inputs you need to produce your products?
Should you expect these input prices to rise or fall in the near future?
To
answer important questions like these, you need to understand the economic
meaning of the demand
for a good. Organisations that understand demand and the factors that influence
demand can respond optimally to changes in the demand for their products or the
products they rely on as inputs.
Law of Demand
The
demand for a good refers to the relation between the price of a good and the
quantity of the good that consumers will be willing and able to purchase at
various prices, holding all other factors that affect purchase decisions
constant.
The law of demand states that other things being equal, as the price of a good increases,
the quantity demanded of that good decreases.
This is true both for the individual
consumer's demand and the market demand for a good, because the market consists
of many individual consumers.
For example,
suppose that through a combination of market research and data from pricing
experiments, a manager at Ekina Sports estimates that
at a price of $100 per pair, consumers would purchase, or "demand",
10,000 pairs of Ekina running shoes each week. The
manager further estimates that consumers would demand 15,000 pairs per week if
the price were decreased to $80, and 20,000 pairs per week if the price were
further decreased to $60.
If you assume that the relation between
price (P) and quantity demanded (Qd) continues in a similar fashion for even
higher or lower prices, you can illustrate the demand for Ekina
shoes on a graph.
Start by constructing a demand schedule
that lists various prices and the quantity of shoes consumers would demand at each
price. For example, assume Ekina further estimates
that at a price of $140, consumers would not demand any shoes; at a price of
$120, consumers would demand five thousand pairs; at a price of $100, consumers
would demand ten thousand pairs, and so on.

Then draw x- and y-axes and show
price (P) on the y-axis and the quantity of shoes demanded (Q) on the x-axis.
You can plot the price-quantity pairs
(from the demand schedule) on the graph and connect them in a linear fashion to produce the demand line, or
"market demand curve" as it is more generally known.

As you look at the graph, notice how the line slopes downwards,
indicating that as the price of shoes decreases, the quantity demanded
increases. Consumers are willing and able to purchase more shoes at the lower
prices than they were willing and able to purchase at the higher prices.
The following link provides a brief look at how the law of demand
works for energy.
Observing the Law of Demand
Demand
Function
It is
often convenient to express this relation between price and quantity demanded
as a mathematical function. You can write the function in two equivalent ways.
One way expresses price as a function of quantity demanded:
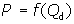
The second way expresses quantity
demanded as a function of price:
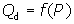
You read the function above:
"quantity demanded is a function of price," not, "quantity
demanded equals f times P." Quantity demanded depends on
price; it is the dependent variable. P is
the independent variable.
What does the demand function tell
you?
The following linear function
summarises the relation between price and quantity demanded represented by the
Demand Schedule and Market Demand Curve above:
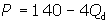
For a reminder of what linear functions
and their properties are, click on the link below.
Analytical Methods: Linear Functions
Notice how this function reflects the
information in the graph below. For example, substituting a
quantity of ten thousand pairs of shoes for Qd results in a price
of $100, which indicates that consumers would demand ten thousand pairs of
shoes at a price of $100 per pair.

You can express the same relation
between price and quantity demanded with quantity demanded on the left side of
the function. Rearranging the same equation to isolate quantity demanded yields:
Q = 35 - P/4
Notice how the conversion maintains the
underlying relation between price and quantity demanded. Substituting $100 for
price results in Qd
= 10 (thousand) as before.
The function
Qd = 35 - P/4
is formally called a demand function because it
expresses quantity demanded as a function of price.
The function
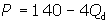
is called the inverse demand function because it
represents the same demand relationship, just inverted. Because both equations
represent the same demand relationship, many economists refer to either as just
the demand function.
You will often use the demand function
with price on the left side because it is consistent with the way economists
represent demand graphically. That is, it reflects the placement of price on
the y-axis and quantity demanded on
the x-axis. This subject will adhere
to this practice throughout.
Generally, you can express the demand function for any linear demand as
a
= the y-intercept
-b = the slope of the function
Notice that a
corresponds to the price at which quantity demanded becomes zero, and b indicates the change in price that
will generate a one-unit change in quantity demanded. In practice, you will
often estimate these parameters using the statistical technique regression
analysis. Regression analysis involves collecting real observations on two
variables, such as P and Q, and then using these observations to
estimate a mathematical relation between the two variables.
If you want to review the mathematics of constants, variables and
coefficients, click on the link below.
Analytical Methods: Constants, Variables and Coefficients
The information contained in a simple
demand equation should not be underestimated. You will find later in the subject
that you can derive a wealth of additional information from a simple demand
equation.
Example:
Demand for coffee
Assume a bakery finds the daily demand function for its coffee to be
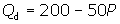
P
= price per cup of coffee
Qd = the
number of cups that consumers would be willing to buy per day at each price
To plot this demand function on a graph,
you first want to solve the demand function for P. Expressing demand in terms of price is consistent with placing
price on the y-axis and quantity
demanded on the x-axis.
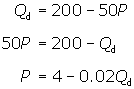
The demand function above has a slope
of -0.02, and a y-intercept of 4. By
substituting values for Qd,
such as 50 and 100, you can find two additional quantity-price pairs (50, $3;
100, $2). You can now plot the pairs, or points, on a graph, with price on the y-axis and quantity demanded on the x-axis.

Click on the
following link for another example of how to draw a linear demand curve.
Example of a Linear Demand Curve
Sometimes
it is better to represent a demand function in a nonlinear form. Before doing
this, you might like to review the mathematics of non-linear functions in the
following link.
Analytical Methods: Nonlinear Functions
You
can take a look at the advanced material in the following link to explore
nonlinear demand functions.
(Advanced) Nonlinear Demand Functions
Other Factors
That Influence Demand
Recall that the law of demand states that other things being
equal, as the price of a good increases, the quantity demanded of that good
decreases. But what if one of the "other things"
changes? For example, how would an economic recession affect the demand
for Ekina shoes? How would an increased marketing
campaign by Ekina affect the demand for its shoes?
What would happen in July if Ekina announced that it
would be raising all of its shoe prices in September in response to increased
costs of rubber and other materials? The demand relationship in each of these
cases would change.
When an important factor other than the price of a good itself changes,
a change in demand for that good may
occur. In the Ekina shoes example, an increase in
demand means that consumers are now willing to purchase more shoes at each
price. Graphically, an increase in demand appears as a rightward (or
"upward") shift of the demand curve.

Similarly, a decrease in demand for Ekina shoes means that consumers are willing to purchase
fewer shoes at each price than previously. Graphically, a decrease in demand
appears as a leftward (or "downward") shift of the demand curve.

Mathematically, an increase or a
decrease in demand appears as an increase or a decrease in the y-intercept a, respectively:
Change in
quantity demanded vs. change in demand
A
change in quantity demanded occurs
when the price of the good alone changes. A change
in demand results from a change in one of the factors other than price.
When price alone changes, no "shift" occurs in the underlying
relationship, you simply move to a higher or lower price-quantity pair along
the same demand curve.
The primary factors that can cause a change in demand (or a shift in the
demand curve) are
·
consumer
income
·
prices of
related goods
·
advertising
and consumer preferences
·
population
·
seasonal
factors
·
expectations
Understanding these factors will allow
you to predict the market response to real economic events.
Test your
knowledge now with an example of a bakery. Click here to begin.
Consumer
income
An increase in consumer income means consumers can afford to purchase
more of all goods. In general, you can expect the demand for most goods to
increase when consumer income increases. The demand for certain items, however,
such as public transportation, may actually decrease as income increases
because consumers can afford more desirable alternatives. A
good for which demand decreases when income increases is an inferior good; a good
for which demand increases when income increases is a normal good.
Prices
of related goods
Changes in the prices of related goods (substitutes
and complements)
lead to changes in demand. A decrease in the price of
a substitute good can cause demand to decrease. For example, assume that ice
cream is a substitute good for frozen yoghurt. A decrease in the price of ice
cream can cause demand for yoghurt to decrease. A decrease in the price of a
complement good can cause demand to increase. For example, if Ekina put its athletic apparel on sale (sports shoes and
athletic wear are complement goods), the demand for its shoes may increase.
Advertising
and consumer preferences
If consumer preferences change so that consumers get more fulfilment from
consuming a good, whether the result of a firm's advertising or outside forces,
demand for the good will increase. Demand for Ekina's
running shoes might increase if Ekina ran commercials
in which Olympic track stars endorsed its shoes, or if a medical report
announced some new health benefits from jogging.
Click here for more information on the importance of brand recognition.
The link here discusses how changes in consumer preferences
impacted upon the demand for energy.
Population
An increase in the population of consumers
will increase demand. For example, as the baby boomer generation ages and the
population of elderly Americans grows, the demand for health care and related
services in the United States will increase.
Seasonal factors
Seasonal factors can also affect the demand
for a product. Buyers purchase certain products heavily during certain times of
the year. For instance, the demand for children's toys will be higher during the
Christmas season (often the fourth quarter) than during other times of the
year.
Expectations
Finally, if consumers' expectations about the price of
a good changes, demand for the good will change. For instance, if consumers
expect prices to rise in the near future, they may demand more of a good today.
The opposite is true if consumers expect prices to fall in the future.
Homebuyers may delay home purchases if they expect the housing market to be
more attractive in a year.
The interactive exercise here
allows
you to see how each of these factors affects the demand curve for another
market - sports drinks.
Topic Summary
In this topic, you have learnt how to
- explain
the law of demand and why demand curves slope downwards
- express demand functions mathematically and graphically
- identify how changes in consumer income, prices of
related good, advertising and consumer preferences, population, seasonal factors
and expectations can cause changes in demand
Now
go on to topic 3.3, “Price Elasticity”.